ISO9001 Certified Professional Manufacturer & Supplier of Optics
+86-0431-87911611 admin@ytoptics.com
Contact us
-
 Email: admin@ytoptics.com
Email: admin@ytoptics.com
-
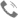 Tel:86-0431-87911611
Tel:86-0431-87911611
-
 Add: 2# Automotive Innovation
Add: 2# Automotive Innovation
Jilin Province, China
Changchun Yutai Optics Co., Ltd.
How to choose an optical mirrors?----Comparison of Internal Reflection & External Reflection
Definition
External Reflection: Reflection occurring at the interface when light travels from a less dense medium to a more dense medium.
Example: Light traveling from air (n≈1.0) to glass (n≈1.5). This is the most common type of reflection in our daily lives.
Internal Reflection: Reflection occurring at the interface when light travels from a denser medium to a less dense medium.
Example: Light traveling from inside glass (n≈1.5) to air (n≈1.0). This phenomenon underlies the operation of optical devices such as fiber optics and prisms.
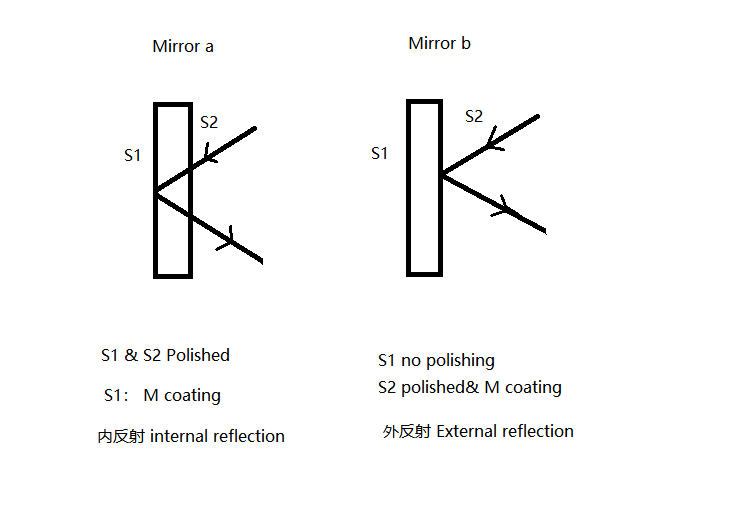
1. Phase Shift (Half-Wave Loss)
This is the most fundamental physical distinction between the two.
External Reflection: When light travels from a less dense medium to a more dense medium, the reflected light undergoes a 180° phase shift, known as “half-wave loss.” This is equivalent to adding half a wavelength (λ/2) to the optical path of the reflected light.
Internal Reflection: During internal reflection, the reflected light does not undergo half-wave loss.
Why is this important? In thin-film interference phenomena (e.g., anti-reflective coatings, anti-glare films) and Newton's rings, half-wave loss is the key factor determining whether interference results in constructive or destructive interference.
2. Critical Angle and Total Internal Reflection
This is the most distinctive and crucial characteristic of internal reflection.
External Reflection: Since refracted light always enters the second medium, no critical angle exists.
Internal Reflection:
When the incident angle < critical angle: Similar to ordinary reflection, both reflected and refracted light exist. This is called partial internal reflection.
When the incident angle ≥ critical angle: Refracted light disappears, and all incident light is reflected back into the first medium. This is called total internal reflection.
Critical angle calculation formula:
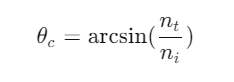
Where ni is the refractive index of the denser medium, and nt is the refractive index of the less dense medium.
External reflection (red line): When the angle of incidence is less than approximately 50°, the reflectance is very low (about 4%). It then rises gradually until it reaches 100% at 90°.
Internal reflection (blue line): Its behavior is nearly identical to external reflection until the critical angle (approximately 41°). Upon reaching the critical angle, the reflectance instantly jumps to 100% and remains constant thereafter, perfectly demonstrating the phenomenon of total internal reflection.
External reflection is common but inefficient (unless the angle of incidence is very large). Mirrors utilize metallic reflection rather than the principle of external reflection.
Internal reflection, particularly total internal reflection, is a highly efficient optical process with negligible energy loss. It forms the foundation of modern optical communications (fiber optics) and serves as the core operating principle for numerous optical instruments, such as the total internal reflection prism in binoculars. Simply put, external reflection is the “standard mode,” while internal reflection possesses the remarkable capability to achieve “perfect reflection” at specific angles.
External Reflection: Reflection occurring at the interface when light travels from a less dense medium to a more dense medium.
Example: Light traveling from air (n≈1.0) to glass (n≈1.5). This is the most common type of reflection in our daily lives.
Internal Reflection: Reflection occurring at the interface when light travels from a denser medium to a less dense medium.
Example: Light traveling from inside glass (n≈1.5) to air (n≈1.0). This phenomenon underlies the operation of optical devices such as fiber optics and prisms.

|
Characteristics |
External Reflection |
Internal Reflection |
|
Refractive Index Condition |
n_i < n_tni |
n_i > n_tni>nt |
|
Phase Change |
Semi-wave loss present |
No semi-wave loss |
|
Critical Angle |
Does not exist |
Exists |
|
Reflectivity |
Increases gradually with increasing angle of incidence |
Similar to external reflection below the critical angle; abrupt change occurs at the critical angle |
|
Energy Distribution |
Reflected and refracted light always coexist |
Divided into two cases: partial reflection and total internal reflection |
|
Common Applications |
Flat mirrors, water surface reflections |
Fiber optics, total internal reflection prisms, anti-reflective coating theory |
1. Phase Shift (Half-Wave Loss)
This is the most fundamental physical distinction between the two.
External Reflection: When light travels from a less dense medium to a more dense medium, the reflected light undergoes a 180° phase shift, known as “half-wave loss.” This is equivalent to adding half a wavelength (λ/2) to the optical path of the reflected light.
Internal Reflection: During internal reflection, the reflected light does not undergo half-wave loss.
Why is this important? In thin-film interference phenomena (e.g., anti-reflective coatings, anti-glare films) and Newton's rings, half-wave loss is the key factor determining whether interference results in constructive or destructive interference.
2. Critical Angle and Total Internal Reflection
This is the most distinctive and crucial characteristic of internal reflection.
External Reflection: Since refracted light always enters the second medium, no critical angle exists.
Internal Reflection:
When the incident angle < critical angle: Similar to ordinary reflection, both reflected and refracted light exist. This is called partial internal reflection.
When the incident angle ≥ critical angle: Refracted light disappears, and all incident light is reflected back into the first medium. This is called total internal reflection.
Critical angle calculation formula:
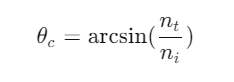
Where ni is the refractive index of the denser medium, and nt is the refractive index of the less dense medium.
External reflection (red line): When the angle of incidence is less than approximately 50°, the reflectance is very low (about 4%). It then rises gradually until it reaches 100% at 90°.
Internal reflection (blue line): Its behavior is nearly identical to external reflection until the critical angle (approximately 41°). Upon reaching the critical angle, the reflectance instantly jumps to 100% and remains constant thereafter, perfectly demonstrating the phenomenon of total internal reflection.
External reflection is common but inefficient (unless the angle of incidence is very large). Mirrors utilize metallic reflection rather than the principle of external reflection.
Internal reflection, particularly total internal reflection, is a highly efficient optical process with negligible energy loss. It forms the foundation of modern optical communications (fiber optics) and serves as the core operating principle for numerous optical instruments, such as the total internal reflection prism in binoculars. Simply put, external reflection is the “standard mode,” while internal reflection possesses the remarkable capability to achieve “perfect reflection” at specific angles.
PREV : Analysing the Core Role of Optical Lenses in Laser Processing NEXT : What are the characteristics and applications of Fused Silica Spherical Lenses?

TALK TO US 86-0431-87911611
86-0431-87911611
Call us now!
 86-0431-87911611
86-0431-87911611Call us now!
ONLINE CHAT
 2433808388
2433808388

